Did you know that while no two snowflakes are exactly the same, they are all six-sided? Snowflakes’ hexagonal shapes are due to the molecular structure of ice.
Snowflake. Image by Wilson A. Bentley.
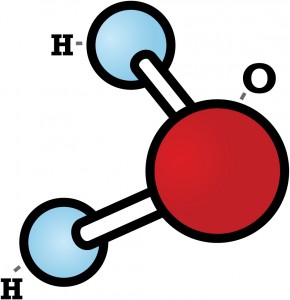
As you might know, each water molecule is made of two hydrogen atoms bonded to one oxygen atom and looks something like this:
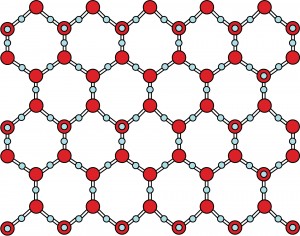
As water freezes, the molecules are forced to align themselves into a very particular structure – a hexagonal lattice that is the basis for the six-sided snowflakes.
This shape also helps explain why water expands as it freezes, while all other solids contract. Ice takes up more space as a solid and is therefore less dense, meaning that ice floats in liquid water. No other compound behaves this way!
Snowflakes in the Classroom
During the winter months, our thoughts turn to all things cold and we often incorporate snow, ice, and even polar bears into our lessons. Teaching about snowflakes can help you meet science and math standards and incorporate art and even children’s literature into your instruction.
Students can read about water and ice in the Beyond Penguins story “Growing Floaters and Shrinking Sinkers” as a part of a lesson or unit or solids and liquids. This story is available at three grade levels: K-1, 2-3, and 4-5 and as text, color books, and electronic books. The version for grades 4-5 includes a suggested activity: modeling water molecules using gumdrops and marshmallows. Students can create edible water molecules and see the resultant hexagonal structure as they align their models to simulate the formation of ice.
Next, students can compare this molecular model to the actual structure of snowflakes. A great place to start is a web site about Wilson “Snowflake” Bentley, the first person to photograph a single snow crystal in 1885. The site includes a collection of original images of snowflakes which could be used in the classroom to illustrate snowflake structure as well as geometric concepts such as symmetry. The children’s book, Snowflake Bentley by Jacqueline Briggs Martin, introduces students to Bentley’s life and work and incorporates the history and nature of science into the lesson.
Finally, students can create their own paper snowflakes to model their hexagonal shape. Many variations on these directions exist, and some even have video instructions! Students can also create snowflakes by cutting and gluing together paper-towel rolls although they should take care to make them six-sided. These activities reinforce the science content and allow students to practice measurement skills and demonstrate an understanding of a hexagon and symmetry.
Snowflakes and Standards
This classic winter craft (and the other suggested activities) can meet many different science and math standards, including:
National Science Education Standards: Grades K-4
Physical Science Content Standard: Properties of Objects and Materials
Materials can exist in different states – solid, liquid, and gas. Some common materials, such as water, can be changed from one state to another by heating or cooling.
Science and Technology Content Standard: Understandings about Science and Technology
Women and men of all ages, backgrounds, and groups engage in a variety of scientific and technological work.
Tools help scientists make better observations, measurements, and equipment for investigations. They help scientists see, measure, and do things they could not otherwise see, measure, and do.
History and Nature of Science: Science as a Human Endeavor
Men and women have made a variety of contributions throughout the history of science and technology.
Many people choose science as a career and devote their entire lives to studying it. Many people derive great pleasure from doing science.
National Council of Teachers of Mathematics Standards
Geometry
Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships.
Apply transformations and use symmetry to analyze mathematical situations.
Measurement
Apply appropriate techniques, tools, and formulas to determine measurements.
This article was written by Jessica Fries-Gaither. For more information, see the Beyond Penguins and Polar Bears Contributors page. Email Kimberly Lightle, Principal Investigator, with any questions about the content of this site.
Copyright August 2011 – The Ohio State University. This material is based upon work supported by the National Science Foundation under Grant No. 0733024. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. This work is licensed under an Attribution-ShareAlike 3.0 Unported Creative Commons license.
